Cryptographie – Partie II – Cryptographie Classique
Temps de lecture : 11 minute(s)
Dans cet article, je passerai en revue les grandes étapes de la cryptographie classique, en m’attardant sur celles qui l’ont révolutionnée.

Origines de la Cryptographie
L’origine de la cryptographie remonte à l’antiquité, soit dès la généralisation de l’usage de l’écriture.
Elle résulte aussi de l’organisation sociale qui prévalait alors : la cité-état (polis). Cette organisation sociale nettement plus hiérarchisée que tout ce qui existait auparavant s’articulait autour du protecteur de la cité qui deviendra bien vite le roi. Avec le pouvoir viennent les richesses, et le besoin de protéger celles-ci contre tout ennemi.
Sachant que la prospérité d’une cité suscitait inévitablement la jalousie des voisines, on comprend qu’elles étaient bien souvent en conflit.
Alliances, trahisons, fédérations de cités, conquêtes. Ces tractations, bien souvent secrètes amenèrent le besoin d’échanger des messages dont seul l’envoyeur et le destinataire pourraient comprendre le sens, afin de ne pas risquer qu’il tombe en de mauvaises mains.
On comprend ici que la cryptographie a d’abord été inventée comme un instrument du pouvoir. Raison pour laquelle les gouvernements, aujourd’hui encore, la considèrent comme une arme[1]
Histoire de la cryptographie
Vous trouverez maintes sources sur internet détaillant l’histoire de la cryptographie depuis l’antiquité jusqu’à nos jours.
D’une manière générale, celle-ci se subdivise en deux grandes étapes, dont la première, la cryptographie classique se termine vers 1970. Après cette date, on parle de cryptographie moderne.
Cyptographie classique
Atbash
Elle débute réellement vers le Vème siècle av. J.-C. avec le premier chiffrement par substitution, inventé par les Hébreux, l’Atbash. Le principe est simple, on inverse l’alphabet. Ainsi A devient Z, B devient Y, etc. Il est symétrique en ce sens qu’appliquer deux fois le chiffrement revient à encrypter puis décrypter le texte original.
Ainsi le texte : EXEMPLE UTILISANT ATBASH Devient : VCVNKOV FGRORHZMG ZGYZHS
C’est un chiffrement faible, dans la mesure où il suffit de connaître l’astuce pour pouvoir déchiffrer n’importe quel message.
Carré de Polybe
Vers 150 avant notre ère, l’historien grec, Polybe décrit un chiffrement par substitution d’un caractères par ses coordonnées dans un tableau.
Code de César
Vers -60, César utilise un code pour communiquer avec ses généraux. Il s’agit d’un décalage de l’alphabet. Prenons un exemple : si la clé est 3
Texte clair (1) : CORRUPTISSIMA REPUBLICA PLURIMAE LEGES Texte Chiffré : FRUUXSWLVVLPD UHSXEOLFD SOXULPDH OHJHV
(1) : Les lois sont très nombreuses lorsque l’Etat est très corrompu
On additionne tout simplement 3 au rang de la lettre, ainsi C devient F, O devient R, et ainsi de suite. Pour décrypter, on soustrait la clé.
Ce type de chiffrement est également faible, puisqu’il n’existe que 25 clés possibles.
Al-Kindi

Vers l’an 900, un savant arabe du nom d’Al-Kindi décrivait, dans ce qui allait devenir le premier traité de cryptanalyse, une méthode permettant de casser les chiffrements monoalphabétiques par analyse fréquentielle.
Il s’agit d’une découverte fondamentale qui reste la base de la plupart des attaques visant à casser les chiffrements. En somme, Al-Kindi avait remarqué que pour une langue donnée, la fréquence des caractères n’est pas égale. Certains caractères sont beaucoup plus fréquents que d’autres, et que cette fréquence est constante sur un texte suffisamment long.
Dès lors, une simple analyse statistique permet de casser les chiffrements dits monoalphabétiques.
Prenons un petit exemple, supposons le cryptogramme suivant dont on sait qu’il a été rédigé en français :
SL CHPZZLHB HYYPCHPA HB IVBA KL SH ALYYL, HB JVBYZ WYVMVUK KL S'VJLHU. SH ZVUA SL WHFZ LA SH CPSSL KLZ JPTTLYPLUZ, JVBCLYAZ KL IYBTLZ LA KL UBLLZ; QHTHPZ SL ZVSLPS, WLUKHUA XB'PS IYPSSL, UL SLZ CPZPAL KL ZLZ YHFVUZ, UP XBHUK PS SLZ YLAVBYUL KB JPLS CLYZ SH ALYYL; BUL UBPA THBKPAL LZA LALUKBL ZBY JLZ TPZLYHISLZ TVYALSZ. HYYPCLZ SH, UVBZ LJOVBVUZ SL CHPZZLHB, UVBZ KLIHYXBVUZ SLZ ILALZ; LA, ZBPCHUA SL JVBYZ KL S'VJLHU, UVBZ HYYPCVUZ UVBZ-TLTLZ HB SPLB XBL T'HCHPA KPA JPYJL.
En procédant à l’analyse statistique, c’est-à-dire au comptage des lettres on voit que c’est la lettre L qui vient en tête avec 63 occurences (16,94%). Comme d’autre part on sait qu’en français c’est la lettre E qui est la plus fréquente, on postule d’un décalage de L-E, soit 7. Et on trouve :
LE VAISSEAU ARRIVAIT AU BOUT DE LA TERRE, AU COURS PROFOND DE L'OCEAN. LA SONT LE PAYS ET LA VILLE DES CIMMERIENS, COUVERTS DE BRUMES ET DE NUEES; JAMAIS LE SOLEIL, PENDANT QU'IL BRILLE, NE LES VISITE DE SES RAYONS, NI QUAND IL LES RETOURNE DU CIEL VERS LA TERRE; UNE NUIT MAUDITE EST ETENDUE SUR CES MISERABLES MORTELS. ARRIVES LA, NOUS ECHOUONS LE VAISSEAU, NOUS DEBARQUONS LES BETES; ET, SUIVANT LE COURS DE L'OCEAN, NOUS ARRIVONS NOUS-MEMES AU LIEU QUE M'AVAIT DIT CIRCE.
Alberti
Vers 1460, Leon Battista Alberti propose la première méthode de chiffrement polyalphabétique, à l’aide d’un cadran chiffrant. La méthode, bien qu’incomplète parce que ne permettant pas l’usage d’une clé est révolutionnaire et représente la plus grande avancée dans le domaine depuis plus de mille ans.
Dans un chiffrement polyalphabétique, une lettre sera représentée tantôt par une lettre, tantôt par une autre, ce qui complique singulièrement la cryptanalyse fréquentielle.
Vigenère
 C’est à Blaise de Vigenère (diplomate français) que l’on doit le premier chiffrement polyalphabétique à clé secrète, qui porte son nom. En réalité, il n’est pas l’inventeur du procédé qui est un dénommé Giovan Battista Bellaso. Duquel s’était inspiré Giambattista della Porta où il semble que Vigenère ait largement puisé son inspiration (sans jamais le citer d’ailleurs – ce qui constituait déjà à l’époque un outrage et une indélicatesse).
C’est à Blaise de Vigenère (diplomate français) que l’on doit le premier chiffrement polyalphabétique à clé secrète, qui porte son nom. En réalité, il n’est pas l’inventeur du procédé qui est un dénommé Giovan Battista Bellaso. Duquel s’était inspiré Giambattista della Porta où il semble que Vigenère ait largement puisé son inspiration (sans jamais le citer d’ailleurs – ce qui constituait déjà à l’époque un outrage et une indélicatesse).
Comment cela fonctionne : il s’agit d’alphabets de substitution basés sur une clé littérale, gardée secrète.
Supposons l’exemple suivant :
Texte clair : NOUS ATTAQUERONS LES POSITIONS ENNEMIES DEMAIN A L'AUBE EN PASSANT PAR LA PORTE SUD. Et que la clé soit : "FORTUNE"
Initialement, le chiffrement et le déchiffrement proposé par Vigenère s’appliquait à l’aide d’une grille, appelé carré de Vigenère.
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| B | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A |
| C | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B |
| D | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C |
| E | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D |
| F | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E |
| G | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F |
| H | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G |
| I | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H |
| J | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I |
| K | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J |
| L | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K |
| M | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L |
| N | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M |
| O | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N |
| P | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O |
| Q | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P |
| R | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q |
| S | S | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R |
| T | T | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S |
| U | U | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T |
| V | V | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U |
| W | W | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V |
| X | X | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W |
| Y | Y | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X |
| Z | Z | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y |
Ainsi, pour encrypter la première lettre du texte qui est N avec la première lettre de la clé qui est F, nous choisissons dans le tableau la colonne N. Puis nous descendons jusqu’à la ligne F, ce qui nous donne S. Et ainsi de suite, en considérant la clé comme circulaire, c’est-à-dire que quand vous avez utilisé le dernier caractère de la clé, vous retournez au premier.
Le résultat, appelé cryptogramme sera :
SCLL UGXFELXLBRX ZVL JBWNHZHHF ISBVFCRW ISDTCA E Q'OLUY RR UOJLUAX UOI EU CSWHV LOQ
Pour décrypter, vous sélectionnez la colonne F (première lettre de la clé), puis vous descendez jusqu’à rencontrer le S dans cette colonne, et vous retrouvez en tête de cette ligne la lettre N.
A cette méthode manuelle correspond une méthode mathématique simple basée sur les rotations permettant d’implémenter ce chiffrement dans un programme informatique.
Il existe également deux formes de variantes qui peuvent être utilisées conjointement et rendent le chiffrement encore plus fort.
- La méthode autoclave : on choisit une clé, mais lorsque l’on a épuisé celle-ci, au lieu de retourner au début, on utilise le texte en clair lui-même comme clé. Dans notre exemple la clé deviendrait : FORTUNENOUSATTAQUERONSL…
- Utilisation d’alphabets arbitraires : consiste à placer les lettres de l’alphabet dans un ordre différent, selon une méthode choisie. Kryptos en est un exemple célèbre. Dans ce cas l’alphabet utilisé était : KRYPTOSABCDEFGHIJLMNQUVWXZ
Cryptanalyse du Chiffre de Vigenère
Le chiffre de Vigenère ne fût cassé qu’en 1863 avec la publication des travaux (restés largement ignorés à l’époque) d’un officier Prussien, Friedrich Wilhelm Kasiski.
Vous l’aurez compris, chaque lettre étant chiffrée par une lettre différente (clé circulaire), il n’est pas trivial de retrouver la clé par analyse fréquentielle.
Mais le fait que la clé soit cyclique, combiné à la longueur du texte fait que inévitablement dans certains passages du cryptogramme certaines lettres auront été chiffrés avec le même morceau de clé.
Partant de là, le but était d’identifier tout d’abord la longueur de la clé.
Cela étant fait (on a une candidate probable, disons), on peut découper le cryptogramme en autant de sous-textes qu’il y a de lettres dans la clé… Et y appliquer les méthodes standard d’analyse fréquentielle. Dans chaque sous-texte la lettre la plus présente doit être le « e », et ainsi de suite.
Chiffrement par tansposition
Ensuite, ce sera l’âge d’or d’une autre forme de chiffrement, par transposition, et non plus par susbtitution. Avec ou sans clé littérale.
Dans une transposition, on déplace les lettres pour rendre le message incompréhensible.
Si nous prenons un simple exemple :
NOUS ATTAQUERONS LES POSITIONS ENNEMIES DEMAIN A L'AUBE EN PASSANT PAR LA PORTE SUD
Et que nous le réécrivons en prenant la première lettre (N) puis la dernière (D), puis la seconde (O) et l’avant-dernière (U), nous obtenons :
NDOUUSS EATTRTOAPQ UAELR ORNASP LTENSA SPSOASPI TNIEO NESB UEAN'NLE MAI ENSI ADME
RailFence et Skip sont deux autres exemples de chiffrement par transposition.
>> Testez vous-même (transpositions)
Vernam : un cas à part
Le chiffre de Vernam, appelé aussi OTP (one time pad) ou masque jetable est un chiffrement inventé par Gilbert Vernam en 1917 et perfectionné par Joseph Mauborgne.
C’est un cas un peu particulier en ce sens que bien qu’étant fondamentalement basé sur simple technique de susbtitution polyalphabétique, c’est le seul chiffrement réputé (et prouvé) impossible à déchiffrer.
Pourquoi ? Parce que la clé est aussi longue que le texte à chiffrer, et qu’elle ne sera utilisée qu’une et une seule fois d’oû le nom de masque jetable.
C’est également le chiffrement le moins pratique qui soit puisqu’il nécessite, pour pouvoir transmettre un secret, de transmettre (en toute sécurité) une clé au moins aussi longue que celui-ci – et qui ne pourra servir qu’une seule fois. La plupart du temps les clés étaient acheminées par porteur (valise diplomatique, officiers de sécurité, etc.).
Petite anecdote
Je vous livre ici un souvenir personnel qui illustre bien l’une des principales failles en cryptographie : l’implémentation.
Qu’il s’agisse de logiciels ou d’humains, le problème est rarement causé par les méthodes cryptographiques elles-mêmes (la théorie) mais découle de la manière dont elles sont mises en pratique.
Au début des années 1990, l’Armée Belge (dans laquelle je servais comme milicien travaillant aux transmissions), on utilisait encore des vieux TELEX à deux bandes perforées : l’une pour le message, l’autre pour la clé.
Ce procédé est appelé Vernam, ou One Time Padding. Il consiste à réaliser un XOR logique entre le texte clair et une bande contenant une clé qui soit au moins aussi longue que le message. Le texte de la clé étant secret et supposé utilisé une seule fois, le cryptogramme ainsi produit était inattaquable.
En pratique, l’opérateur envoyant un message téléphonait à son homologue et lui disait quelle bande il devait utiliser. Les deux « montaient » la bande-clé sur le telex, puis la transmission avait lieu et le message arrivait tout décrypté chez le récepteur. So far, so good.
Le hic, c’est que dans mes souvenirs, on n’avait que 5 bandes différentes. Pour l’OTP, vous repasserez. Evidemment les petits génies de l’état-major, qu’on espère plus versés dans l’art de la guerre que celui des mathématiques n’avaient pas vu qu’en réutilisant la clé, ils commettaient une erreur fatale. Ils donnaient (pratiquement) la clé à toute personne ayant pu intercepter plus d’un cryptogramme encrypté avec celle-ci.
En effet, supposons les textes secrets T1 et T2 respectivement encryptés avec la clé K, qui donneront C1 et C2.
C1=T1 XOR K
C2=T2 XOR K
Alors… C1 XOR C2 = T1 XOR T2. Le fait de combiner les deux cryptogrammes par la fonction XOR nullifie la clé, et il ne reste que la combinaison par XOR des deux documents, bit à bit.
Une des meilleures démonstrations de ceci est visuelle.
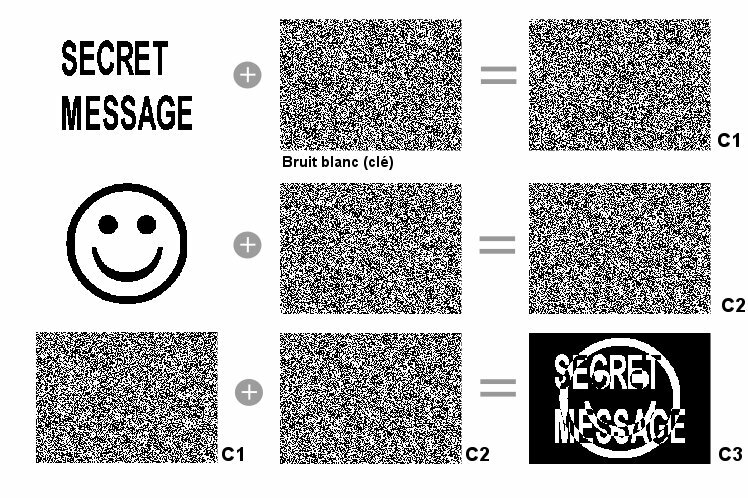
- Première ligne : on encrypte point à point via l’opérateur OU exclusif une image contenant un message « SECRET MESSAGE » avec la clé, qui est en l’occurence un bruit blanc, c’est-à-dire des points plus ou moins au hasard. On obtient C1 qui est en effet indéchiffrable
- Seconde ligne : on refait l’opération, avec un smiley, cette fois. Le résultat (C2) est tout aussi indéchiffrable.
- Troisième ligne : si un attaquant a pu se procurer les deux cryptogrammes C1 et C2, il peut les recombiner (C3) via le même opérateur, et le résultat est cette fois pratiquement clair. L’élément aléatoire de la clé a été annulé par l’opération, et ce qui reste n’est que la combinaison par l’opérateur OU exclusif des deux images secrètes.
Cette méthode, appliquée à du texte, permet de réduire l’attaque à une simple analyse fréquentielle, encore une fois. On sait que certaines suites de lettres sont plus fréquentes que d’autres. On pose qu’elle est présente à tel endroit, et si ce qui résulte d’un XOR entre cette suite et le cryptogramme est également intelligible (et globalement cohérent du point de vue des fréquences), c’était un bon « candidat ». Avec les ordinateurs actuels, un jeu d’enfant.
Notez que c’était déjà de cette manière que les Américains avaient réussi à casser des milliers de pages de messages émanant du Bloc Soviétique entre 1940 et 1948. Cette opération, gardée secrète jusqu’en 1995 portait le nom de Projet Venona, et avait notamment permis de démanteler des réseaux d’espions soviétiques infiltrés.




